FAM at Stellenbosch University

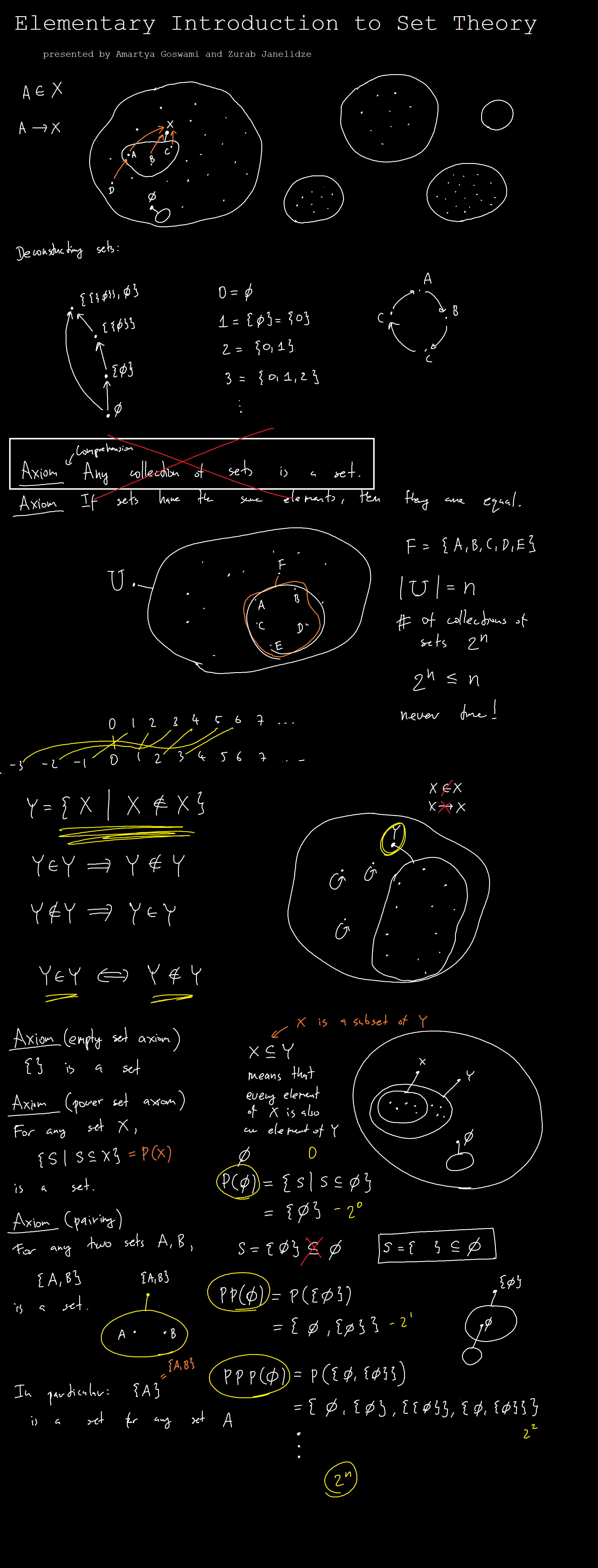
What is FAM?

"FAM" is an acronym for an undergraduate course, "Foundations of Abstract Mathematics", offered by the Department of Mathematical Sciences of Stellenbosch University (FAM I and FAM II, respectively) since 2012/2011. The course consists of two year-long modules, FAM I (Mathematics 278) and FAM II (Mathematics 378), offered at the second and the third year, respectively. It is possible to enroll for only one of the two modules. Neither of the modules has any prerequisites, although note that admission to the third-year module is subject to approval by the Department of Mathematical Sciences. The course aims to let the students experience mathematical research, at the level corresponding to students' mathematical skills, and in this process, to uplift those skills.

A bit of history

When teaching a course in calculus at the University of Cape Town in 2008, Zurab Janelidze was approached by a student, Pieter du Toit, with a request to show him mathematics beyond what was taught in the course. This led to a Seminar in Pure Mathematics, which was run by Zurab and attended by Pieter and some of his friends. When Zurab was appointed as a lecturer at Stellenbosch University in 2009, he offered Ingrid Rewitzky and Karin Howell to jointly run a seminar, based on the model of the Seminar in Pure Mathematics, for undergraduate students. The enthusiasm of students attending this seminar led to the conception of the Foundations of Abstract Mathematics modules, based on a framework proposed by Ingrid and Zurab. Thanks to the support of the Head of the Mathematics Division at the time, David Holgate, the third-year module was introduced in 2011, and the second-year module in 2012. The Faculty approved this initiative under the understanding that lecturers involved in teaching these modules would do so in their free time instead of it being part of their official teaching workload. Teaching of these modules became part of the official teaching load by the initiative of the new Division Head, Florian Breuer, a few years after the introduction of the modules. He, Zurab, and Stephan Wagner were the main lecturers in the module for several years, until the resignation of Florian and Stephan (who took up academic positions in Australia and Sweden, respectively). During these years, the module was convened by Zurab. In 2023, the module is jointly convened by Zurab and Sophie Marques. A majority of postgraduate students in Mathematics at Stellenbosch University, who have completed their undergraduate studies at SU, would have followed one or both of the FAM modules during their undergraduate studies. For some of them, these modules played a crucial role in inspiring them to switch their existing career choice (e.g., engineering, computer science, theoretical physics) to mathematics. There are examples where ideas conceived in FAM I and FAM II have led to research topics at the Honors, Masters and PhD levels. 

FAM assignments

Assessment in FAM is mainly based on assignments, where students need to apply their creativity to solve problems not discussed in class (or tutorial), compose proofs of theorems, sometimes in a symbolic language (in a formal proof system), come up with examples or counterexamples to a concept/hypothesis, or come up with their own theorems (and their proofs). Occasionally, some of these assignments involve coding proofs using a proof assistant software. Students who show readiness for engaging with a mathematical exploration project (a longer version of the usual assignment), which often comes close to an honors project in terms of its quality and content, are given the opportunity to engage with a longer project in the place of smaller assignments. 

The following is a fragment of a conversation among a group of students who were required to append this recording, discussing their semi-joint assignment, to the latter (rewind to play the full video - but its long!). Note that the recording is shared with the permission of all students in the video.

How do students find the experience?

The video above ends with the group members discussing how FAM has impacted them. Here is what some of the other students have said when asked what they have learned in the first quarter of the FAM module in 2021 (once again, shared under permission):

• Reading and understanding equations. We knew about logical operators, but now we know how to use them more effectively to get actual results. This equips one with a toolbox to use in other math modules. Reading and interpreting equations in other modules specifically.
• A philosophical look at mathematics: instead of being given a problem and asked to solve it, now we look at the mechanics of how we can solve the problem and what really encompasses mathematical activity. Comparison with language is fascinating. It is a good life skill to understand logic, which this term contributed to.
• Originally, I thought of this like every other math course: numbers and calculations. Now I view this course more as a course in logic which teaches you how to think. This was very cool, very unlike to what I have done before. Excellent pacing: it was important not to go fast to get a good understanding of what we are working on.
• This term gave me a deeper understanding of mathematics - it was not just about learning a method and solving problems. It was nice that in the beginning more emphasis was placed on effort rather than accuracy. Instead of trying to get it right, one had the opportunity to engage deeper and learn more about the subject, than in other modules where the emphasis is to learn something to get it right. In this module, you learn to understand. The focus was more on understanding concepts rather than grasping the language used to interpret the concept.
• Usually, the student is on the receiving end - now it is the student who was expected to produce a precise mathematical statement that others would be able to interpret correctly.
• The concept of breaking things down and unpacking in proofs. A cool skill to learn. Mathematics is neither invented or discovered. Mathematics is rather something that is within every human being.
• How anything can be turned into math. Mathematics can be made from a normal conversation. How to write down logical reasoning through mathematical steps.
• How mathematics is really so broad around us. I kind of new this, but I did not realise the actual broad extent if this.
• The seminar does not force you to parrot learn - it is much more understanding based. It is a nice thing that the focus is on understanding the work.
• Instead of repetitive information, the lecturer gives us information and lets us build on it while learning from each other. I wish other modules were like that too.
• This is probably the only course that brings thought into it. After the lecture, instead of being happy that the lecture is done, you are still thinking about the lecture. Assessments reflect this too. Putting in extra thought and creativity gives you marks. So assessments allow thought input. You also have the freedom to interpret things in your own way.
• This module teaches you how to formulate your thoughts and structure them in terms of assumptions and conclusions. You must think carefully and understand the process, rather than go through everything step by step or parrot learning, as is often the case in other math modules.

See https://foabma.blogspot.com/ for further feedback.

The Abstract Mathematics stream

A few years ago, FAM has inspired creation of a new focal area (aka stream) within the BSc Mathematical Sciences programme. It features FAM I and II as compulsory modules, among other mathematics modules at the second and third year levels. This stream gives students flexibility to combine a mathematics major with majors in biochemistry, chemistry, physics, genetics, computer science, applied mathematics, and mathematical statistics (only four major combinations are possible in all other focal areas of the programme).  

Read More

Fundamano

 

Read More

The Proof Course: Lecture 2

Many real-life situations lead us to considering a mathematical problem dealing with finding all possible numbers \(x\) satisfying a certain formula. In most primitive cases, this formula is an equation involving basic arithmetic operations (like the one we considered in Lecture 1). As an example of a formula that does not fall in this category, consider the following one:

\(x<y^2\) for every value of \(y\) (Formula A)

In other words, the formula expresses the property that no matter what value of \(y\) we pick, we will always have \(x<y^2\). Let us write this purely symbolically as follows (so that it looks more like a formula!):

\(y\Rightarrow x<y^2\) (symbolic form of Formula A)

In general, the symbol "\(\Rightarrow\)" describes logical implication of statements. Here the implication is: if \(y\) has a specific value then \(x<y^2\). In the symbolic form above, the assumption that \(y\) has a specific value is expressed by just writing \(y\) on the LHS (left-hand-side) of the implication symbol "\(\Rightarrow\)". Since we are not giving any further detail as to which specific value does \(y\) have, the implication must not be dependent on such detail, and hence the RHS (right-hand-side), \(x<y^2\), must hold for all values of \(y\). Note however that this type of symbolic forms, where variables are allowed to be written on their own like in the LHS of the implication symbol above, is not a standard practice. We will nevertheless stick to it, as it makes understanding proofs easier. 

So, what is the solution of Formula A? If \(x<y^2\) needs to hold for every value of \(y\), then in particular, it must hold for \(y=0\), giving us \(x<0^2=0\). This can be written out purely symbolically, as a proof:

1. \(y\Rightarrow x<y^2\)
2. \(x<0^2\)
3. \(x<0\)

However, as we know from Lecture 1 already, this proof only proves that if Formula A is true then \(x<0\). In order for \(x<0\) to be the solution of Formula A, we also need to prove that if \(x<0\) then Formula A is true. Well, since \(0\leqslant y^2\) is true for every \(y\), combining \(x<0\) with \(0\leqslant y^2\) we will get \(x<y^2\), as required in Formula A. So the proof is:

1. \(x<0\)
2. \(y\Rightarrow 0\leqslant y^2\)
3. \(y\Rightarrow x<y^2\)

Note that it seems as if this proof violates our requirement that in a basic proof, every line except the first one must be a logical conclusion of the previous one or several lines. Line 2 does not necessarily seem to be a conclusion of Line 1. Instead, it is simply a general true fact that does not seem to logically depend on Line 1 at all: it says that the square of every number is greater or equal to \(0\). We can account for such situations by agreeing that "several" in "one or several lines" includes the case of "\(0\) many". So in a basic proof we can also include lines that recall facts we know. If we had not done that in the above proof, we would have to skip from Line 1 directly to Line 3, and it may not have been so clear how does one logically conclude Line 3 from Line 1. So we allow inclusion of known facts as lines in a basic proof for the sake of clarity. Knowing this, we might want to make the first proof clearer by inserting one such line:

1. \(y\Rightarrow x<y^2\)
2. \(x<0^2\)
3. \(0^2=0\)
4. \(x<0\)

Read More

The Proof Course: Lecture 1

In this blog-based lecture course we will learn how to build mathematical proofs.

Let us begin with something simple. You are most likely familiar with "solving an equation". You are given an "equation", say \[x+2=2x-3\] with an "unknown" number \(x\) and you need to find all possible values of \(x\), so that the equation holds true. You then follow a certain process of creating new equations from the given one until you reach the solution: \[2+3=2x-x\] \[5=x\] This computation is in fact an example of a proof. To be more precise, there are two proofs here: one for proving that

if \(x+2=2x-3\) then \(x=5\) (Proposition A),

and the other proving that

if \(x=5\) then \(x+2=2x-3\) (Proposition B).

The first proof is the same as the series of equations above. The second proof is still the same series, but in reverse direction. The two Propositions A and B together guarantee that not only \(x=5\) fulfills the original equation (Proposition B), but that there is no other value of \(x\) that would fulfill the same equation (Proposition A). It is because of the presence of these two proofs in our computation that we can be sure that \(x=5\) is indeed the solution of the equation \(x+2=2x-3\).

In general, a proof is a series of mathematical formulas, like the equations above. However, in addition to a "vertical" structure of a proof, where each line displays a formula that has been derived from one or more previous lines, there is also a "horizontal" structure, where each line of a proof has a certain horizontal offset. This is, at least, according to a certain proof calculus formulated by someone by the name of Fitch. There are other ways of defining/describing proofs; in fact, there is an entire subject of proof theory, which studies these other ways. We will care little about those other ways and stick to the one we started describing, as it is closest to how mathematicians actually compose proofs in their everyday job.

So where were we? We were talking about "vertical" and "horizontal" structure of a proof. Not to complicate things too much at once, let us first get a handle on the vertical structure of proofs, illustrating it on various example proofs that have most primitive possible horizontal structure. We will then, slowly, complexify the horizontal structure as well.

For Proposition A, the proof goes like this:

1. \(x+2=2x-3\)
2. \(2+3=2x-x\)
3. \(5=x\)

The numbers at the start of each line are just for our reference purposes, they do not form part of the proof. Line 2 is a logical conclusion of Line 1: if \(x+2=2x-3\) then it must be so that \(2+3=2x-x\), since we could add \(3\) to both sides of the equality and subtract \(x\) as well – a process under which the equality will remain true if it were true at the start.

Line 3 is (again) a logical conclusion of Line 2: since \(5=2+3\) and \(2x-x=x\), so if the equality in Line 2 were true then the equality in Line 3 must be true as well.

A series of lines of mathematical formulas where every next line is a logical conclusion of the previous one or more lines, is a mathematical proof with simplest possible horizontal structure. We will call such proofs "basic".

Proposition B also has a basic proof:

1. \(5=x\)
2. \(2+3=2x-x\)
3. \(x+2=2x-3\)

Just as before, every next line is a logical conclusion of the previous one.

What about the first line (in each proof)? If the first line were to also satisfy the requirement that it is a logical conclusion of the previous lines, then, since there are no lines before the first line, it would appear that the first line is true on its own, without a need for justification. If course, in both proofs this is false: in the first proof, we cannot claim that Line 1 is true. Truth of Line 1 in the first proof depends on the value of \(x\). Without knowing anything about the value of \(x\), we cannot claim that \(x+2=2x-3\), since if, say, \(x=0\), then \(x+2=2x-3\) is clearly false. The same for the second proof - we cannot claim that Line 1 is true. Instead, the role of the first line in each of the proofs is to "assume" they are true, and then see what conclusions can be drawn from such assumption. Recall that Proposition B, for instance, states that if \(x=5\) then \(x+2=2x-3\). It does not state that 

\(x=5\) and \(x+2=2x-3\), 

or that 

\(x=5\) or \(x+2=2x-3\), 

and so on. So in a basic proof the first line will always be an assumption, unlike the rest of the lines, which are conclusions from the previous one or several lines.

Read More

Bracket Notation for Mathematical Proofs

The bracket notion for mathematical proofs is an adaptation of the Fitch notation for Gentzen's natural deduction proof system. It has led to the development of the SOFiA proof assistant. This post brings together some videos explaining the bracket notation and the first-order formal language for mathematics in the context of the bracket notation.

1. General Overview

~ 20 min

2. Building Blocks for Statements

~ 1 hour

3. Examples of Forming Statements

~ 40 min

4. Examples of Forming Statements (Continued)

~ 35 min

5. Concluding Quantified Statements

~ 35 min

6. Concluding from Quantified Statements

~ 1 hour

Read More

Category Theory 2022 - an NGA course

Here you will find the content for the Category Theory course given under the National Graduate Academy NGA-Coursework of the CoE-MaSS. The lectures are on Saturdays 9:00-11:00. 

Register here to receive the Zoom link for joining the lectures

There is also a Discord channel for this course, which you can find on the Discord server of the NGA-Coursework project. 

This is a video-based course aimed at post-graduate students and as well academics interested to learn about category theory, with live participation of the audience shaping the content of the course. For a reading course at the South African honors level, see:

• Category Theory: A First Course by George Janelidze

For an introduction to category theory for non-mathematicians and undergraduate students, see:

• Elementary Introduction to Category Theory by Amartya Goswami and Zurab Janelidze 

Lecture 1: Categories

Lecture 2: Functors

Lecture 3: Natural Transformations

Lecture 4: Adjunctions

Lecture 5: Limits

Lecture 6: Duality

Lecture 7: Yoneda Embedding

Lecture 8: Equivalence of Categories

9. Exponentiation

10. Universal constructions

Read More

Mathematical Structures Course 2022

This page contains resources for a SATACS course at NITheCS that runs over the second semester of 2022. The lectures take place on Zoom on Fridays 17:00-19:00. If you would like to join them, register here.

Lecture 1: Magmas

Lecture 2: Join Semi-Lattices

Lecture 3: Relations

Lecture 4: Universes

Lecture 5: Posets

Lecture 6: Groups

Lecture 7: Topological Spaces

Lecture 8: Posets II

Lecture 9: Posets III

Read More

Elementary Introduction to Set Theory

This is the blog post of the 2022 August NITheCS Mini-School. Let us begin with some useful links:

• Lecture notes on universes of sets (introductory) 
• Some videos explaining the concepts from the lecture notes above

Lecture 1

Lecture 2

Lecture 3

Lecture 4

Read More

Python-Based Introduction to Mathematical Proofs

Scroll down for video lectures

1. What is a Mathematical Proof?  

Mathematical proof is a method of discourse which allows a human being to: 

• discover new mathematical knowledge,
• analyze existing mathematical knowledge,
• verify truthfulness of a piece of mathematical knowledge. 

The ability to construct a mathematical proof is part of human nature. It is closely related to the ability to form thoughts and reason.

Mathematical knowledge is knowledge of abstract principles about our universe. As such, it requires use of symbols to represent entities that are inherently abstract. For example, the symbol 2 may represent 2 apples or 2 pears. The number 2 is an abstract entity, since it is not confined to any of these concrete representations. 

Mathematics functions at different levels of abstraction too. For instance, we may write a symbol, such as n, to represent any number. In one case we could have n = 2, and in another case we could have n = 3. This is a second layer of abstraction compared to the layer of each specific number, such as number 2. Symbols representing abstract entities form basic ingredients of mathematical proof. The most complex parts of mathematical proofs deal with manipulations of these symbols, which sometimes may take an extremely long time. To optimize a proof, it is important to understand its most fundamental components. The aim of these lectures is to provide an exposition of these fundamental components. 

Activity. Get Python IDE, if you do not already have one: there are many available, Spyder is recommended (very easy to install). Then, get the file sofia.py, which can be obtained from https://github.com/ZurabJanelidze/sofia. Save sofia.py to the runtime directory of your Python IDE. To test that you have done it correctly, create a separate file named something.py, copy-paste the following code in that file, and run the file with your Python IDE:

import sofia

sofia.help()

Read More

Lectures

• Calculus (notes in progress in Real Variable Calculus)
• NITheCS Mini-School on Elementary Introduction to Category Theory, a series of lectures for the October Mini-School at the South African Mini-School in Theoretical and Computational Sciences, given jointly with Amartya Goswami
• Abstract Algebra for the Future Mathematician, a book in progress jointly with Amartya Goswami
• The Caravan this is an introductory book in progress on foundations of abstract mathematics.
• My inaugural lecture publication and the lecture.
• See the mathematics playlist of my youtube channel for my video lectures.
• Cardinal Arithmetic (Cantor’s theory of cardinality for Grothendieck-type universes)
• Morphisms of finite spaces (introduction to the basic ideas of category theory via topology and combinatorics)
• Posets and connections (introduction to Galois connections)
• Homomorphisms of monoids (includes products, sums and quotients of monoids)
• Universal algebra (Birkhoff’s variety theorem and some Mal’tsev conditions)
• Abstract logic (work in progress)
• Categories (extremely basic introduction to categories)
• Universal properties (a prelude)
• Regular categories (basics)
• An abelian exploration of diagram lemmas (notes for the lectures delivered under the Erasmus+ program in 2018 at the University of Lovain-la-Neuve)
• Calculus of exact sequences (notes for the lectures delivered under the Erasmus+ program in 2017 at the University of Lovain-la-Neuve)
• Written lecture # 100 on Laplace transform
• Written lecture # 101 on Laplace transform (second part)
• Written lecture # 102 on basic constructions with sets
• #103 on real vector spaces
• #104 on equivalence relations
• #105 types of continuous functions
• #106 constructions with topologies
• #108 open interval topology
• #109 linear maps and the eigenvalue problem
• #110 homeomorphisms
• Incidence relation (a small fragment of Euclid-Hilbert axiomatic geometry)
• Universes of Sets (a first course on axiomatic set theory based on the work of Zermelo)
• Relations (includes functions as defined by Dedekind, equivalence relations and partial orders)
• Natural Arithmetic (axiomatic development of the natural number system within set theory, following Dedekind and Peano)
• #111 the concept of unit fraction

Read More